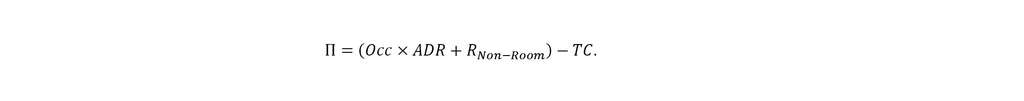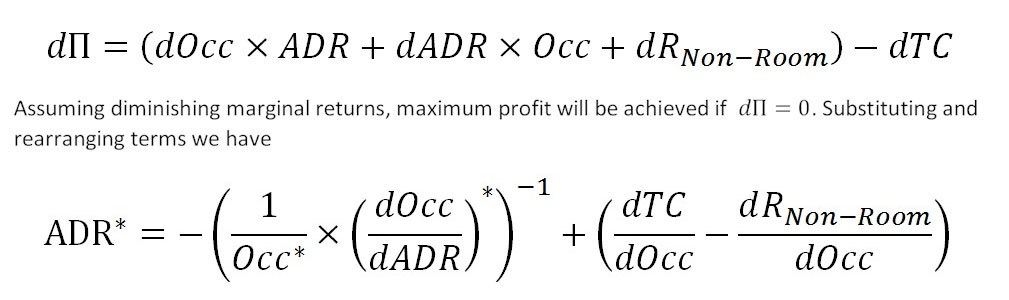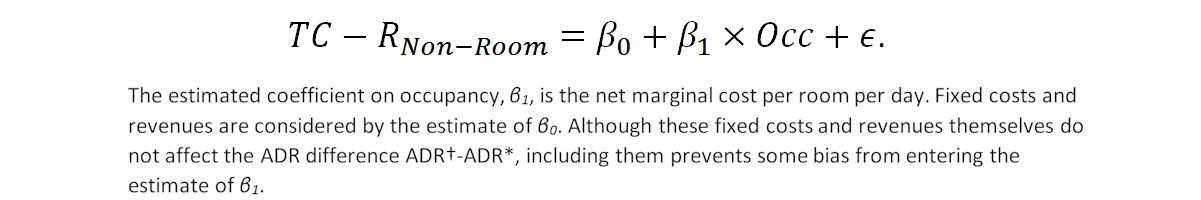Hotel Statements: A Model of Profit Maximizing Premia and Discounts
Rooms revenue per available room, reported as RevPAR, is perhaps the most scrutinized performance indicator in the hotel business. Although the true aim of a hotel's operation is to maximize profit, the wide availability and frequent reporting of RevPAR may make revenue the hotel manager's most immediate target. Revenue-maximizing is simpler to estimate and requires less information than profit-maximizing.
Specifically, no knowledge of the hotel operations is needed for revenue maximizing, only knowledge or beliefs about demand. For some situations, achieving revenue goals may be sufficient to increase profits, further entrenching the strategy of revenue maximizing.
Recently, increasingly tight margins and more sophisticated management practices have turned attention to bottom-line measures. Aligning the incentives of revenue managers and hotel owners requires a thorough understanding of the differences in the two approaches.
In this paper, I will formulate a model of the hotel business that makes these differences explicit. Then, examining hotel profit and loss statements from different groups of hotels, I will estimate the scale of the differences in ADR that result from the two strategies in different types of hotels.
Theoretical Considerations
The profit of the hotel can be described by the equation:
where TR is total revenue and TC is total cost. To distinguish between the RevPAR maximizing firm and the profit maximizing firm, it is useful to break the total revenue into the RevPAR component and the non-rooms component, producing the per-room, per-day profit equation:
Taking the total derivative yields:
where stars indicate optimal values for profit maximizing. The optimal price has two parenthetical components, the inverse semi-elasticity of occupancy with respect to rate and the net balance of changes to costs and non-rooms revenue for some additional occupancy. This first term, the inverse semi-elasticity term, is a measure of how sensitive potential guests are to ADR changes. Less sensitive guests will tolerate higher ADR than more sensitive ones.
This term also reflects that each individual hotel has some power to control its prices-i.e. the hotel will not completely empty with the slightest price increase. Some travelers may decide to stay elsewhere with a higher price, and some will pay the extra amount. Therefore, the price the hotel manager will set depends on the sensitivity its guests have to price as well as the balance of the second term.
The second term, made up of the difference in marginal costs and marginal non-rooms revenue, is intuitively straightforward to grasp. Each additional percentage point of occupancy may produce additional costs from staffing, cleaning, laundry and utilities. Additional occupancy also means that there are more guests to produce non-rooms revenues from food and beverage, guest laundry or the spa.
If the costs predominate, it is in the hotel manager's interest to raise prices. This reduces the total number of guests that incur additional costs while ensuring that the remaining guests each pay the more generous rate. On the other hand, the hotel manager will want to lower rates, potentially below the cleaning (variable operating) costs, if the non-rooms revenue produced by the additional guests is sufficiently high.
Rooms revenue maximizing is performed in the same manner, without costs and non-rooms revenue. This produces:
where daggers indicate optimal values for revenue maximizing. Although the semi-elasticity term looks identical to that of the profit maximizer, when facing the same group of potential guests, the terms will only be equivalent if either the marginal costs are exactly equal to the marginal non-rooms revenues or if both are zero.
A manager that maximizes RevPAR will also maximize profit if the hotel's operations approximate these conditions. A hotel conventionally represents a relatively large fixed investment-the hotel itself-and marginal costs may be close to zero or low enough to be offset by some incidentals. This is particularly true if there is some slack in the labor inputs. However, if there are important non-room revenue components, or the marginal costs become significant as the slack is taken up through managing efficiencies and increasingly scarce labor, revenue maximizing becomes a less accurate proxy strategy of profit maximizing.
For the cases where the marginal costs and non-rooms revenues are significant, the semi-elasticity term will also differ. Guests become more price-sensitive as prices increase and less price sensitive as prices decrease, so the semi-elasticity will tend to offset price changes motivated by marginal costs and non-rooms revenues. For example, high marginal costs above non-room revenues motivate an ADR premium over the revenue-maximizing price. The higher price increases price sensitivity among guests. The resulting net optimum premium still increases ADR, but by less than the full amount of the marginal costs.
Conversely, if non-rooms revenue motivates lower ADR, decreasing price sensitivity will allow the manager to attract extra guests with less than the full discount. The consistency of changes in the direction of price sensitivity means that the effect of occupancy on the balance of marginal non-room revenues and costs can be estimated to establish upper or lower bounds on the premium or discount that should be applied to a revenue maximizing ADR to produce the profit-maximizing ADR for groups of hotels.
Empirical Findings
The differences in the solution rates for the two strategies, ADR†-ADR*, can be approximated by estimating the effect of occupancy on the balance of expenses and non-room revenues:
This estimation makes a few simplifying assumptions. First, it assumes that the costs of accommodating another guest room are constant over the entire range of feasible occupancies. This may not be true if resources (chiefly labor) become increasingly scarce with higher occupancies.
Secondly, this estimation does not account for the elasticity component described earlier. If a manager suddenly considers cost, it's almost certainly true that 100% of the cost cannot be laid directly on consumers in the form of higher prices. Conversely, consumers will not receive the full amount of non-room revenue in the form of lower room rates. In either case, the additional expenses or incomes will be split between the hotel and the guests according to the consumer's elasticity.
In this sense, the model estimated from Equation 6 presents the opposite problem from the revenue-maximizer. Whereas the revenue maximizer does not account for costs but only consumer preferences, Equation 6 only accounts for costs and not consumer preferences. Therefore, the true premium or discount from the revenue maximizing result will lie somewhere between zero and the estimate produced with this model.
The model described by Equation 6 can still be used to estimate the direction of the price change as well as relative magnitudes among different groups of hotels. Estimation is carried out using the CBRE Hotels Trends
® data, a database of around 120,000 hotel operating statements collected between 1994 and 2018. There is a potential for large biases to occur in the estimation due to omitted variables related to occupancy.
I mitigate some of these concerns through the use of a fixed-effects panel estimator that will control for time invariant differences. Hotels are also subsampled to isolate specific hotel groups. The hotels are here classified by property type and STR chain scale but could be grouped in any number of arbitrary ways. Exhibit 1 presents the results of the analysis in table form.
Overall, most of the coefficient estimates on occupancy are quite precise, with some exceptions. The simplest of the property types to interpret are the extended stay hotels. With few if any chances for non-rooms revenue, the marginal cost of letting one more room increases with the chain scale and, presumably, with the level of service. All chain scale segments of extended stay should maintain prices above revenue-maximizing levels, with higher segments raising prices proportionally higher.
Limited-service hotels, with a correspondingly limited opportunity for non-rooms revenue, follows a similar pattern, although the balance of costs and non-rooms revenue for an additional room is very nearly the same across upper midscale, upscale, and upper upscale hotels. This may be due to the chief differences in the segments resting in the fixed costs rather than marginal costs or due to expanded opportunities for non-rooms revenue in the upper chain scales.
Full-service hotels, on the other hand, have varied effects. With the exception of midscale full-service hotels, the addition of food and beverage revenues from additional guests outweighs the additional expense. Thus, the maximum premium that the manager of a full-service hotel should place on room rates is smaller than for the limited-service counterpart in the same chain scale segment.
Resort hotels, with the exception of upscale resorts, take this even farther. The balance of additional non-rooms revenues and expenses incurred from an additional room for upper midscale, upper upscale and luxury resorts is statistically indistinguishable from zero. In other words, the revenue maximizing ADR is also the profit maximizing ADR for these types of hotels, on average. The point estimates, while not statistically significant, are even negative for upper upscale and luxury resorts, suggesting that the extra non-rooms revenue from an additional guest may more than make up for the cost. In this case, ADR should be lowered from the revenue-maximizing level in order to maximize profit.
Conclusion
The considerations for revenue maximizing and profit maximizing are different in theoretically significant ways. Strictly speaking, the revenue-maximizing manager can completely ignore operations when setting price. Clearly, this has the potential to create a situation where unprofitable stays can be produced. This occurs when the additional costs incurred by the guest are not recouped by the rooms and non-rooms revenues. Conversely, it may be the case that some guests are excluded by ADRs that are too high when these guests are willing to more than make up for the cost of their stay through non-rooms revenues.
The simple statistical model derived from equations 1-5 and described in equation 6 can offer the manager some guidance as to the direction and scale of the price difference. When applied to a large sample of hotel operating statements, this model produced estimates that align with our intuition. Extended stay and limited-service hotels should always raise rates above the revenue maximizing price to increase profits. Full-service hotels should also raise rates, but frequently by a smaller amount. Resort hotels, with ample opportunities for non-rooms revenue, should maintain the revenue-maximizing ADR, or even lower ADRs to attract more guests.
The statistical model presented here is generalizable to any group of hotels and is seemingly robust enough to generate plausible estimates; however, this model has a significant limitation. It only estimates the operations portion of the manager's problem and ignores the demand elasticity. This provides only an upper limit on the price differential. Further research on demand elasticity could unite the two approaches, providing a two-part model that gives an estimate centered on the actual premium or discount that the profit-maximizing manager should apply to the revenue-maximizing price.